
dp처럼 배열에서 조건에 맞는 값들을 이전값과 비교하여 하나씩 처리해가지만,
dp배열을 추가적으로 필요로는 하지 않는 문제.
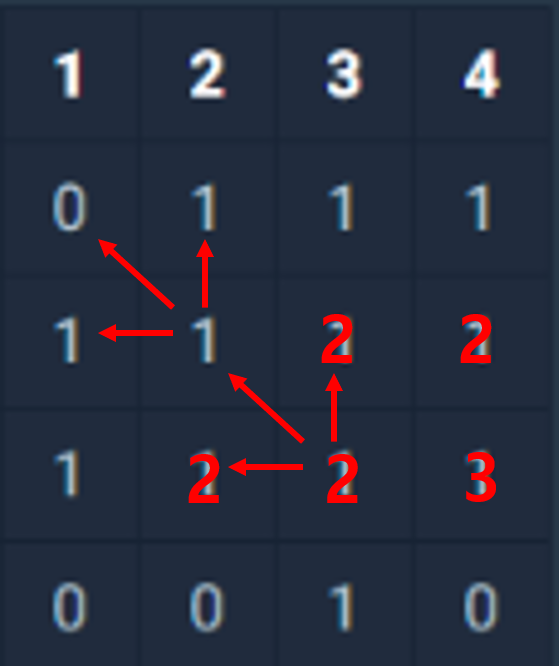
그림처럼 현 인덱스의 좌, 상, 좌상의 값이 모두 1이상이면 정사각형이라고 판단되어 진다.
이 때, 좌, 상, 좌상값중 가장 작은 값에 +1 한 값을 현 index에 더해준다. (변이 하나 늘었음을 의미한다.)
인덱스의 값의 제곱한 값이 곧 정사각형의 넓이가 된다.
예시는 최대값 3인 넓이 9의 정사각형을 리턴한다.
그리고 넓이가 1인 경우에는 하나라도 1이 있다면 1을 리턴해주면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
function solution(board)
{
var answer = 0;
const ylength = board.length;
const xlength = board[0].length;
if (ylength < 2 || xlength < 2) {
for(var i = 0 ; i < ylength ; i++){
for(var j = 0; j < xlength ; j++) {
if (board[i][j] === 1) {
return 1;
}
}
}
}
let max = 0;
for(var i = 1 ; i < ylength ; i++){
for(var j = 1; j < xlength ; j++) {
if(board[i][j] === 1 ){
board[i][j] =
Math.min(board[i - 1][j], board[i][j - 1], board[i - 1][j - 1]) + 1;
if (board[i][j] > max) {
max = board[i][j];
}
}
}
}
return Math.pow(max, 2);
}
|
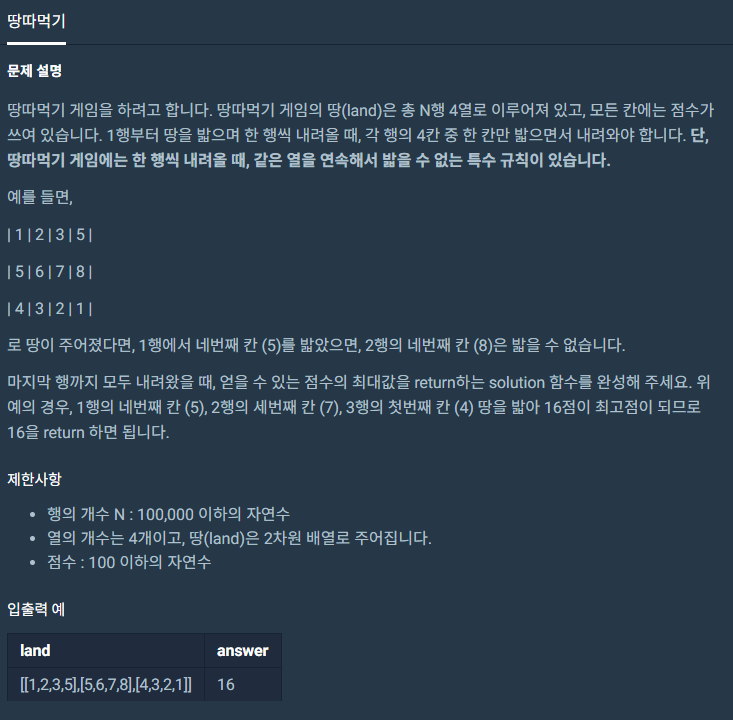

전형적인 dp문제
dp[i][0] = max(dp[i-1][1],dp[i-1][2],dp[i-1][3]) + land[i][0]
dp[i][1] = max(dp[i-1][0],dp[i-1][2],dp[i-1][3]) + land[i][1]
dp[i][2] = max(dp[i-1][0],dp[i-1][1],dp[i-1][3]) + land[i][2]
dp[i][3] = max(dp[i-1][0],dp[i-1][1],dp[i-1][2]) + land[i][3]
두번째 줄부터
조건에 만족할 수 있는 케이스 중에 가장 높은 케이스를 찾는다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
function solution(land) {
var answer = 0;
const dp = Array(land.length).fill(null).map(()=>Array(4).fill(0));
for(let i =0; i<4; i++) {
dp[0][i] = land[0][i];
}
for(let i =1; i<land.length; i++) {
for(let j = 0; j<4; j++) {
for(let k = 0; k<4; k++) {
if(j!=k){
dp[i][j] = Math.max(dp[i][j] , dp[i-1][k]+land[i][j])
}
}
}
}
for(let i =0; i<4; i++) {
answer = Math.max(answer,dp[land.length-1][i])
}
return answer;
}
|
'Algorithm' 카테고리의 다른 글
| [스택/큐2] 기능개발, 주식가격, 계산기 (0) | 2019.07.27 |
|---|---|
| [스택/큐] 프린터, 탑, 쇠막대기, 다리를 지나는 트럭 (0) | 2019.07.26 |
| [완전탐색] 소수 찾기 (0) | 2019.07.17 |
| [탐욕법] 체육복, 구명보트 (0) | 2019.07.09 |
| [DP] N으로 표현, 타일 장식물, 정수 삼각형 (0) | 2019.07.07 |



