N으로 표현

계속해서 추적해야 하는 값이 수의 케이스이기 때문에 배열을 리턴한다.
d[n] = n개를 사용하여 만든 수의 모음
d[n] 은 d[n-i] + d[i] ( 이 때, i는 1부터 n-1) 까지
이 때 중복된 값은 딱히 제거하지 않아도 상관없으나,
말 그대로 중복해서 계산하기 때문에 중복을 무시하기 위해 set을 이용한다.
마지막으로 목적하는 값이 있다면 해당 인덱스를 리턴한다.
아닌 경우에는 -1을 리턴한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include <string>
#include <vector>
#include <unordered_set>
using namespace std;
int N;
unordered_set<int> cache[10];
unordered_set<int> solve(int n) {
if (!cache[n].empty()) return cache[n];
int num = 0;
for (int i = 0; i < n; i++) num = 10 * num + N;
unordered_set<int> res;
res.insert(num);
for (int i = 1; i < n; i++) {
auto s1 = solve(i);
auto s2 = solve(n - i);
for (int n1 : s1) {
for (int n2 : s2) {
res.insert(n1 + n2);
res.insert(n1 - n2);
res.insert(n1 * n2);
if (n2 != 0) res.insert(n1 / n2);
}
}
}
return cache[n] = res;
}
int solution(int _N, int number) {
N = _N;
for (int i = 1; i <= 8; i++) {
solve(i);
if (cache[i].find(number) != cache[i].end()) return i;
}
return -1;
}
|
타일 장식물
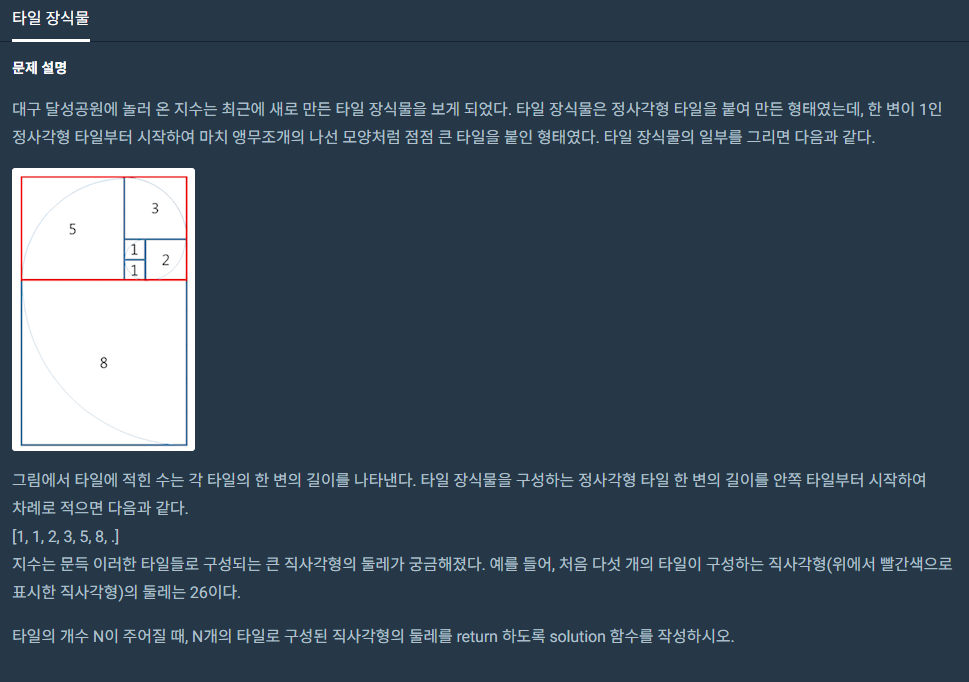
dp문제인데
dp 배열을 만들면 효율성에서 실패한다.
dp가 여러 경우에 대해서 처리해야 하는 경우가 아니라
오로지 하나의 경우에만 현재값, 전값, 전전값을 알면 된다면
dp배열을 만들 필요가 없다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#include <string>
#include <vector>
using namespace std;
int dp[81] = {0, };
long long solution(int N) {
long long answer = 0;
if(N == 1) return 4;
dp[1] = 1;
dp[2] = 1;
for(int i=3; i<=N; i++){
dp[i] = dp[i-1] + dp[i-2];
}
return (dp[N] + dp[N - 1] + dp[N]) * 2;
}
|
< 효율성에서 실패한다 >
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
#include <string>
#include <vector>
using namespace std;
int dp[81] = {0, };
long long solution(int N) {
long long answer = 0;
long long dp1 = 1;
long long dp2 = 1;
long long dp3 = 0;
if (N ==1){
return 4;
}else{
for(int i=3; i<=N; i++){
dp3 = dp1 + dp2;
dp1 = dp2;
dp2 = dp3;
}
}
return (dp2 + dp1 + dp2) * 2;
}
|
< 효율성에서 성공한다 >
정수 삼각형

dp배열 안에는 지나 갈 수 있는 경로중 최대 값을 입력 해야 한다.
이 때 dp배열은 정수삼각형 배열과 같은 크기로 해주지 않을 경우 메소드를 통하지 않고는 접근하기 힘들어서 꼭 배열로 지정 해두는 것이 좋다.
또 최대가 될수 있는 케이스가 두가지인 경우에
최대값을 얻기 위해 max()메소드를 사용하는 것을 익혀두자.
dp[deep][spot] = max(
dp[deep-1][spot-1] + a[deep][spot],
dp[deep-1][spot] + a[deep][spot]
)
이지만 갈수 있는 경로는 대각 오른쪽 한칸 왼쪽 한칸이기 때문에
첫번째 spot과 마지막 spot은 조건을 걸어두지 않으면 indexOf 에러를 발생시킨다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
#include <string>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<vector<int>> triangle) {
int answer = 0;
vector<vector<int>> dp(triangle.size(),vector<int>(triangle.size()));
dp[0][0]=triangle[0][0];
for (int deep = 1; deep < triangle.size(); deep++) {
for (int spot = 0; spot <= deep; spot++) {
if (spot == 0)
dp[deep][spot] = dp[deep - 1][spot] + triangle[deep][spot];
else if (spot == deep)
dp[deep][spot] = dp[deep - 1][spot - 1] + triangle[deep][spot];
else {
dp[deep][spot]
= max(
dp[deep - 1][spot - 1] + triangle[deep][spot],
dp[deep - 1][spot] + triangle[deep][spot]);
}
if (deep == triangle.size() - 1)
answer = max(answer, dp[deep][spot]);
}
}
return answer;
|
'Algorithm' 카테고리의 다른 글
| [완전탐색] 소수 찾기 (0) | 2019.07.17 |
|---|---|
| [탐욕법] 체육복, 구명보트 (0) | 2019.07.09 |
| [힙(Heap)] 더 맵게, 라면 공장, 이중 우선순위 큐 (0) | 2019.07.05 |
| [Hash] Map(STL Container) 이해하기 (완주하지 못한 선수, 위장) (0) | 2019.07.05 |
| [정렬2] ABC, 수열 정렬, 전화번호부 목록,거북이 (0) | 2019.07.04 |



