DFS/BFS

그래프 검색은 다음과 같은 특징을 지닌다.
1. 배열간의 연결들로 이루어진 배열을 지닌다.
2. 방문에 대한 기록을 가지는 배열을 지닌다.
3. 연결되어 있고 방문하지 않은 노드들에 대하여 Search를 진행한다.
DFS의 경우는 위의 특성과 더불어 다음과 같은 특성을 가진다.
1. 재귀 함수를 이용한다. ( 스택도 사용한다고 하지만 아직 보지 못함 )
2. 재귀 함수를 사용하기 때문에 첫번째 요소의 방문 여부는 함수 밖에서 처리한다.
3. 이를 이용하여 깊이 우선으로 탐색한다. (가능한 끝까지 모든 연결된 자식노드 먼저 처리)
BFS의 경우는 그래프 특성과 더불어 다음과 같은 특성을 지닌다.
1. queue를 이용한다.
2. 함수안에서 첫번째 요소에 대한 방문여부를 지정한다.
3. 이를 이용하여 너비 우선으로 탐색한다. (현재 노드에서 갈수 있는 노드부터 점차적 처리)
그 외에 queue의 사용방법이나
vector의 값 초기화 등을 알아두자!
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
using namespace std;
const int MAX = 1000 + 1;
int N, M, V;
int adjacent[MAX][MAX];
vector<bool> visited(MAX,false);
queue<int> q;
void DFS(int idx) {
cout << idx << " ";
for (int i=1; i<=N; i++)
if (adjacent[idx][i] && !visited[i]) {
visited[i] = true;
DFS(i);
}
}
void BFS(int idx) {
q.push(idx);
visited[idx] = true;
while (!q.empty()) {
idx = q.front();
q.pop();
cout << idx << " ";
for (int i=1; i<=N; i++)
if (adjacent[idx][i] && !visited[i]) {
visited[i] = true;
q.push(i);
}
}
}
int main(void) {
cin >> N >> M >> V;
for (int i = 0; i < M; i++) {
int from, to;
cin >> from >> to;
adjacent[from][to] = 1;
adjacent[to][from] = 1;
}
visited[V] = 1;
DFS(V);
cout << "\n";
visited = vector<bool> (MAX,false);
BFS(V);
cout << "\n";
return 0;
}
|
< 소스 코드 >
타켓 넘버

이진트리 형식으로 생각 해보고 접근 할 수 있다.
모든 N의 깊이 만큼의 트리가 있을 경우
0 ~ N 까지 1 과 -1 를 자식노드로 가지는 노드가 있고
해당 노드들을 내려가면서 하나씩 더해주면 모든 경우에 수를 탐색 할 수 있다.
문제의 예에서는
n[0]과
(n[0] * -1) 를 리프노트로 가지는 이진 트리이고
깊이를 하나씩 늘려가며 합을 구한다.
이 때, 이진 트리는 모두 연결되어 있기 때문에
반복문을 사용하여 연결되어있는지 여부를 판단하지는 않는다.
그리고 일반적으로 끝이 있는 DFS에 비해 해당 문제는 끝이 없다.
( 사이즈가 정해져 있어 for문 만큼만 돈다 던지 그런게 없어서 무한루프 )
그래서 모든 경우( 원하는 깊이까지 도달 했을 경우 )를 마칠 시에
sum 과 target을 비교하여 결과를 찾는다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#include <string>
#include <vector>
using namespace std;
int answer;
void dfs(vector<int> numbers, int target, int sum, int deep) {
if(deep >= numbers.size()) {
if(target == sum)
answer++;
return;
}
dfs(numbers,target, sum + numbers[deep], deep + 1);
dfs(numbers,target, sum - numbers[deep], deep + 1);
}
int solution(vector<int> numbers, int target) {
dfs(numbers,target,numbers[0],1);
dfs(numbers,target,numbers[0]*-1,1);
return answer;
}
|
< 소스 코드 >
네트워크
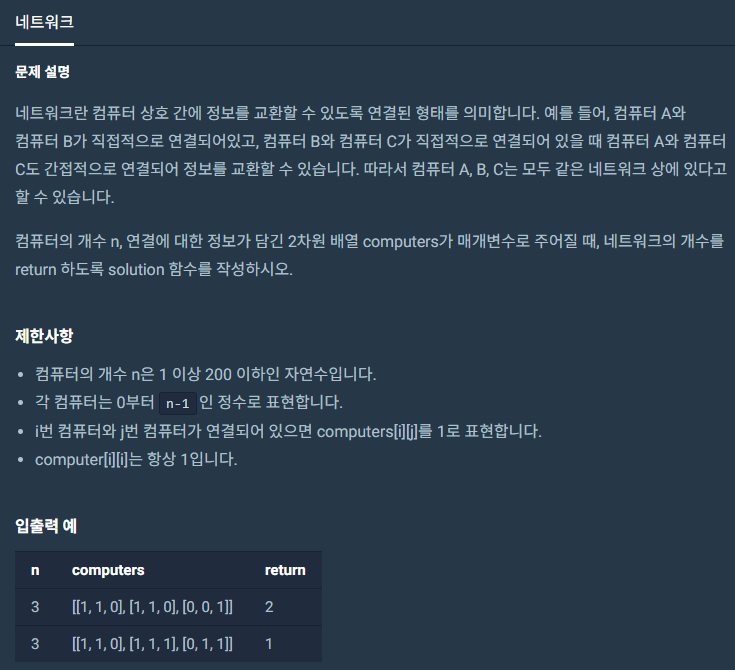
전형적인 그래프 탐색으로 연결한 노드를 찾는 문제이다.
다만 모든 그래프가 연결되어 있지 않기 때문에
반복문을 돌려 방문하지 않은 그래프를 모두 탐색해야 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
#include <string>
#include <vector>
using namespace std;
bool check[200];
void dfs(int target, int n, vector<vector<int>> computers){
for(int i=0; i<n; i++) {
if(!check[i] && computers[target][i]) {
check[target] = 1;
dfs(i,n,computers);
}
}
return;
}
int solution(int n, vector<vector<int>> computers) {
int answer = 0;
for(int i =0; i<n; i++) {
if(!check[i]) {
check[target] = 1;
answer++;
dfs(i,n,computers);
}
}
return answer;
}
|
단어 변환

풀이 접근 1.
배열의 숫자 대신 문자로 연결되어 있다.
일반적인 방문하지 않고 연결되어 있다면이 아니라
단어 중 하나를 제외한 나머지 모든 문자가 같아야지 연결되어 있다고 판단한다.
풀이 접근 2.
단어는 순서대로 접근하지 않는다. ("dot" 으로 시작 할 수 있음 )
그렇기 때문에 모든 단어에 대해서 dfs를 한번씩 실행하여야 한다.
풀이 접근 3.
for문을 모두 도는 것으로 DFS는 종료된다.
하지만 cur == target인 경우에 목표에 도달했기 때문에
return을 따로 해주어여 한다. 그리고 결과 값 전에 로직을 취한다.
풀이 접근 4.
그 외에 루프나 시간 초과가 걸릴시에
visited.resize()를 통해서 vector에 공간 예약을 해주어 성능 향상을 시도해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#include <string>
#include <vector>
using namespace std;
vector<bool> visited;
int mincnt = 987654321;
void DFS(string cur, const string &target, int cnt, vector<string> &words) { /* 특정 경우 종료
if(cur == target) { //현재 값과 타겟이 같다면 값을 리턴한다. *
mincnt = mincnt > cnt ? cnt : mincnt; // 이 때 가장 짧은 경로를 리턴한다. *
return; ****************/
}
for(int i = 0; i < words.size(); i++) { // 모든 단어를조회
int tmp = 0; // DFS에서 사용할 cntTmp
if(visited[i]) continue; // 방문한 단어는 제외 /* 여기서부터 조건비교
*
for(int idx = 0; idx < cur.size(); idx++) //단어 비교 *
if(cur[idx] != words[i][idx]) tmp++; *
*
if(tmp != 1) continue; // 연결 되어 있지 않다면 PASS * 여기까지 조건 비교 */
visited[i] = true; // 연겷되어 있다면 해당 단어를 방문하고
DFS(words[i], target, cnt+1, words); // 깊이 탐색
visited[i] = false; // 탐색을 모두 마친후 초기화
}
}
int solution(string begin, string target, vector<string> words) {
for(int i = 0; i < words.size(); i++) { // 모든 단어를 조회
int cnt = 0;
for(int idx = 0; idx < begin.size(); idx++) // begin과 words를 비교
if(begin[idx] != words[i][idx]) cnt++;
if(cnt != 1) continue; // 만약 1개를 제외하고 모두 같지 않다면 다음 단어로 못 넘어가므로 해당 단어는 PASS!
visited[i] = true; // 해당 단어 방문 여부 판단
DFS(words[i], target, 1, words); // DFS(현재 words, 타겟, cnt , words)
visited[i] = false; // 탐색을 모두 마친후 첫번째 words 초기화
}
if(mincnt != 987654321) return mincnt;
else return 0;
}
|
유기농 배추

가장 기본적인 dfs 문제이다.
주의해서 볼 점은 c++ 의
memset 메소드
헤더 파일은
<string.h> => memset , sizeof()
memset( 타겟배열, 초기화 할 값, 메모리 크기(바이트 수))
이를 통해 타겟 배열의 메모리 위치부터 메모리 크기까지 전부 초기화할 값을 입력하게 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include <iostream>
#include <string>
#include <algorithm>
#include <string.h>
using namespace std;
int gameCount, x, y, beacu;
int vat[50][50] = {0,};
int check[50][50] = {0,};
int dx[4] = {0,0,-1,1};
int dy[4] = {1,-1,0,0};
void dfs(int targetX, int targetY) {
for(int i =0; i<4; i++) {
int nextX = dx[i] + targetX;
int nextY = dy[i] + targetY;
if(nextX>=x || nextX<0 || nextY >= y || nextY < 0){
continue;
}
if(!check[nextX][nextY] && vat[nextX][nextY]) {
check[nextX][nextY] = 1;
dfs(nextX,nextY);
}
}
}
int main() {
cin >> gameCount;
for(int game = 0; game< gameCount; game++){
cin >> x >> y >> beacu;
memset(vat, 0, sizeof(vat));
memset(check, 0, sizeof(check));
int jirungi = 0;
for(int i=0; i<beacu; i++) {
int beacuX, beacuY;
cin >> beacuX >> beacuY;
vat[beacuX][beacuY] = 1;
}
for(int i =0; i<x; i++){
for(int j= 0; j<y; j++) {
if(!check[i][j] && vat[i][j]){
jirungi++;
check[i][j] = 1;
dfs(i,j);
}
}
}
cout<< jirungi << endl;
}
return 0;
}
|
'Algorithm' 카테고리의 다른 글
| [힙(Heap)] 더 맵게, 라면 공장, 이중 우선순위 큐 (0) | 2019.07.05 |
|---|---|
| [Hash] Map(STL Container) 이해하기 (완주하지 못한 선수, 위장) (0) | 2019.07.05 |
| [정렬2] ABC, 수열 정렬, 전화번호부 목록,거북이 (0) | 2019.07.04 |
| [정렬] K번째 수, 가장 큰 수, H-Index, 수 정렬하기, 나이순 정렬, 단어 정렬 (0) | 2019.07.03 |
| [알고리즘]프로그래머스 - 해시 (0) | 2019.04.12 |


